Percentile

Percentiles

Percentile: the value below which a percentage of data falls.

Example: You are the fourth tallest person in a group of 20

80% of people are shorter than you:

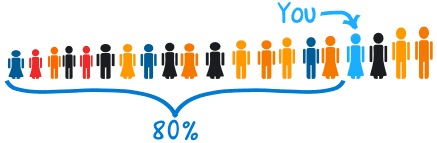
That means you are at the 80th percentile.

If your height is 1.85m then "1.85m" is the 80th percentile height in that group.

In Order

The data needs to be in order!

To calculate percentiles of height the data needs to be in height order (sorted by height).
To calculate percentiles of age the data needs to be in age order.
And so on.

Deciles

A related idea is Deciles (sounds like decimal and percentile together), which splits the data into 10% groups:

• The 1st decile is the 10th percentile (the value that divides the data so that 10% is below it)
• The 2nd decile is the 20th percentile (the value that divides the data so that 20% is below it)
• etc!

Example: (continued)

You are at the 8th decile (the 80th percentile).

Quartiles

Another related idea is Quartiles, which splits the data into quarters:

Example: 1, 3, 3, 4, 5, 6, 6, 7, 8, 8

The numbers are in order. Cut the list into quarters:

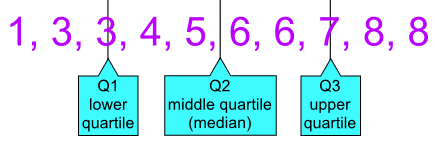
In this case Quartile 2 is half way between 5 and 6:

Q2 = (5+6)/2 = 5.5

And the result is:

• Quartile 1 (Q1) = 3
• Quartile 2 (Q2) = 5.5
• Quartile 3 (Q3) = 7

The Quartiles also divide the data into divisions of 25%, so:

• Quartile 1 (Q1) can be called the 25th percentile
• Quartile 2 (Q2) can be called the 50th percentile
• Quartile 3 (Q3) can be called the 75th percentile

Example: (continued)

For 1, 3, 3, 4, 5, 6, 6, 7, 8, 8:

• The 25th percentile = 3
• The 50th percentile = 5.5
• The 75th percentile = 7

Estimating Percentiles

We can estimate percentiles from a line graph.

Example: Shopping

A total of 10,000 people visited the shopping mall over 12 hours:

Time (hours)	People
0	0
2	350
4	1100
6	2400
8	6500
10	8850
12	10,000

a) Estimate the 30th percentile (when 30% of the visitors had arrived).

b) Estimate what percentile of visitors had arrived after 11 hours.

First draw a line graph of the data: plot the points and join them with a smooth curve:

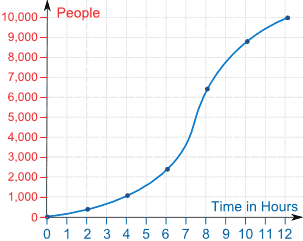
a) The 30th percentile occurs when the visits reach 3,000.

Draw a line horizontally across from 3,000 until you hit the curve, then draw a line vertically downwards to read off the time on the horizontal axis:

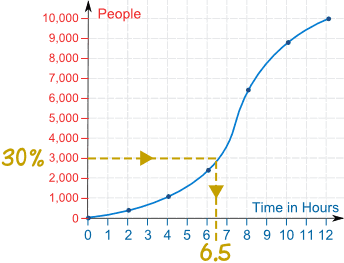
So the 30th percentile occurs after about 6.5 hours.

b) To estimate the percentile of visits after 11 hours: draw a line vertically up from 11 until you hit the curve, then draw a line horizontally across to read off the population on the horizontal axis:

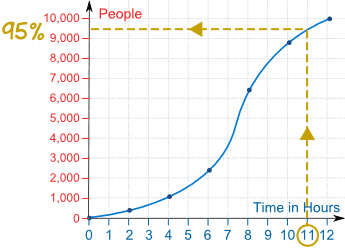
So the visits at 11 hours were about 9,500, which is the 95th percentile.

การหาตำแหน่งข้อมูล

การหาตำแหน่งที่ของข้อมูล ( เปอร์เซ็นไทล์ )  
การหาตำแหน่งหรือลำดับที่ของข้อมูลในแต่ละชุด เช่น นาย A สอบได้ที่ 10 เราไม่สามารถบอกได้ว่าผลการสอบของนาย A เป็นอย่างไรของกลุ่ม ถ้าในกลุ่มของนาย A มีนักเรียน 45 คน ก็สรุปว่านาย A เป็นคนเก่งในกลุ่ม ถ้าในกลุ่มมีเพียง 10 คน ก็สรุปว่านาย A เป็นคนที่เรียนไม่เก่ง และสอบได้ที่สุดท้าย เพื่อช่วยให้การกล่าวถึงตำแหน่งเป็นไปโดยมีความหมาย คือ สามารถบอกได้ทันที่ว่าตำแหน่งนั้นดีไม่ดีเพียงไรในกลุ่ม จึงได้มีการหาวิธีการบอกตำแหน่งโดย บอกตำแหน่งด้วย ควอร์ไทล์  เดไซล์  และเปอร์เซ็นไทล์
           เปอร์เซ็นไทล์  เป็นค่าที่แบ่งข้อมูลออกเป็น 100 ส่วนเท่าๆกัน เมื่อข้อมูลถูกเรียงจากน้อยไปหามาก เนื่องจากค่าที่แบ่งจำนวนข้อมูลออกเป็น 100 ส่วนเท่าๆกัน มีอยู่ 99 ค่า ดังนั้นเราจึงตั้งชื่อแต่ละค่าว่า
           เปอร์เซ็นไทล์ที่หนึ่ง  ใช้สัญลักษณ์ P₁   คือค่าที่มีจำนวนข้อมูลน้อยกว่าค่านี้อยู่ประมาณ 1 ใน100 ของข้อมูลทั้งหมด
           เปอร์เซ็นไทล์ที่สอง  ใช้สัญลักษณ์ P₂  คือค่าที่มีจำนวนข้อมูลน้อยกว่าค่านี้อยู่ประมาณ 2 ใน100 ของข้อมูลทั้งหมด
           จะมีลักษณะเช่นนี้ไปเรื่อยๆจนถึงเปอร์เซ็นไทล์ที่เก้าสิบเก้า ใช้สัญลักษณ์ P₉₉          การหาเปอร์เซ็นไทล์ ก็เช่นเดียวกับการหาควอร์ไทล์และเดไซล์ คือต้องหาตำแหน่งของเปอร์เซ็นไทล์ก่อน ให้ N เป็นจำนวนข้อมูลหรือความถี่ทั้งหมด

           1.กรณีที่ข้อมูลยังไม่แจกแจงความถี่                                                                                       ตำแหน่งของ P₁ คือตำแหน่งที่ ( N + 1)( 1/100 )
           ตำแหน่งของ P₂ คือตำแหน่งที่ ( N + 1)( 2/100 )
           จะมีลักษณะเช่นนี้ไปเรื่อยๆจนถึงตำแหน่งของ P₉₉ คือตำแหน่งที่ ( N + 1)( 99/100 ) 
           โดยทั่วไป ตำแหน่งของเปอร์เซ็นไทล์ที่ r คือ            ตำแหน่งของ P_r คือตำแหน่งที่ ( N + 1 )( r/100 )
            2.กรณีที่ข้อมูลแจกแจงความถี่           ตำแหน่งของ P₁ คือตำแหน่งที่  N( 1/100 )
           ตำแหน่งของ P₂ คือตำแหน่งที่  N( 2/100 )
           จะมีลักษณะเช่นนี้ไปเรื่อยๆจนถึงตำแหน่งของ P₉₉ คือตำแหน่งที่ N( 99/100 )
           โดยทั่วไป ตำแหน่งของเปอร์เซ็นไทล์ที่ r คือ           ตำแหน่งของ P_r คือตำแหน่งที่ ( Nr/100 ) 

          หมายเหตุ การหาเปอร์เซ็นไทล์ เราจะใช้ในกรณีที่มีข้อมูลดังกล่าวมีจำนวนมากๆ เพราะว่าเปอร์เซ็นไทล์เป็นค่าที่แบ่งจำนวนข้อมูลออกเป็น   100   ส่วนเท่าๆกัน     ดังนั้นในกรณีที่ข้อมูลมีจำนวนน้อยไม่เหมาะที่จะหา
เปอร์เซ็นไทล์ควรจะไปใช้ควอร์ไทล์ หรือ เดไซล์จะดีกว่า